Так как окружность касается оси 0X (дано), то
центр окружности находится в точке с координатами О(Xo;R).
Уравнение окружности:
(X-Xo)²+(Y-R)²=R² или в нашем случае
X²-2X*Xo+Xo²+Y²-2R*Y+R²=R² или
X²-2X*Xo+Xo²+Y²-2R*Y=0.
Обе точки должны удовлетворять этому уравнению или
49-14Xo+Xo+64-16R=36-12Xo+Xo+81-18R. Отсюда
Xo=R-2 (координата центра).
То есть центр лежит в точке О(R-2;R).
Тогда уравнение нашей окружности примет вид:
для точки (7;8)
(9-R)²+(8-R)²=R² или
R²-34R+145=0. Решаем квадратное уравнение и получаем
R1=17+√(17²-145) = 17+12=29.
R2=17-12=5
Тогда искомое уравнение:
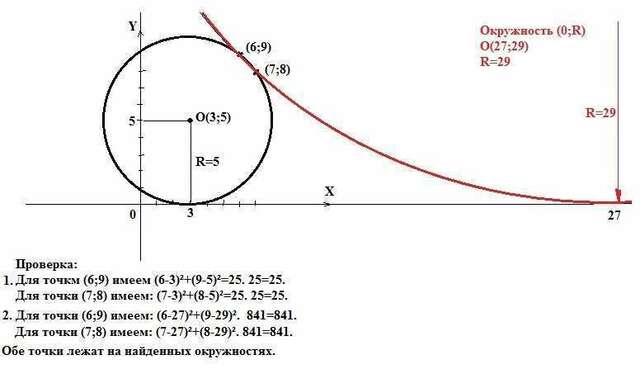
(X-3)²+(Y-5)²=25. (первый вариант).
(X-27)²+(Y-29)²=841. (второй вариант).
Оба уравнения представляют окружности, пересекающиеся в точках
(7;8) и (6;9).