2.
BE+EC=AF+FD (т.к. BE=FD, EC=AF) => BC=AD
∠CEF=∠EFA - являются накрест лежащими, следовательно BC║AD
Значит, ABCD - параллелограмм по первому признаку параллелограмма (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм).
3.
Угол прямоугольника равен 90°. Если взять меньший угол (1) за x, тогда второй угол будет равен 2х. х+2х=90° => х=30°, значит больший угол будет равен 60°. Угол в 30° лежит против меньшей стороны, равной 12 см. Значит, диагональ будет равна 24 см, т.к. сторона, лежащая против угла в 30°, равна половине гипотенузы (а гипотенузой у нас как раз является искомая диагональ).
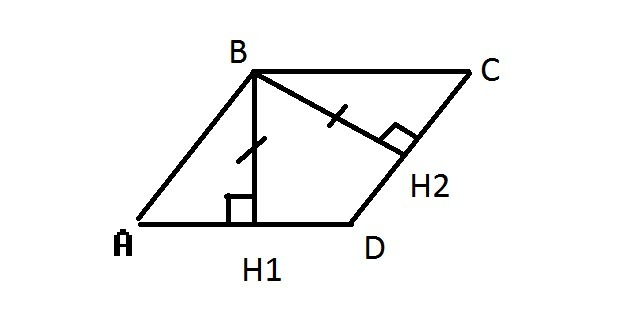
5.
Рассмотрим прямоугольные треугольники ABH1 и BCH2.
У них:
1) ∠А=∠С (противоположные углы параллелограмма равны).
2) BH1=BH2 по условию.
Значит, ΔABH1=ΔBCH2 по второму признаку равенства прямоугольных треугольников.
Следовательно, AB=BC из равенства треугольников. Но противоположные стороны параллелограмма равны (BC=AE, AB=CE). Из этих двух равенств выходит, что AB=BC=AE=CE. Все стороны равны => ABCD - ромб.