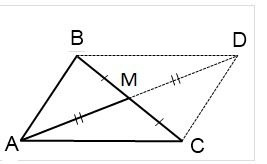
Пусть в треугольнике ABC известны стороны AB=c, BC=b и медиана BM=m.
На луче AM отложим отрезок MD, MD=AM и соединим точку D с точками B и C.Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD — параллелограмм (по признаку). А значит, мы можем применить свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Имеем: BC²+AD²=2(AB²+AC²). Отсюда b²+(2m)²=2(c²+AC²), b²+4m²=2c²+2AC², AC²=(b²+4m²-2c²)/2.
Подставляем значения и имеем: AC² =(4 + 4*9 - 2*4)/2 = 20/2 = 10
AC = sqrt(10)