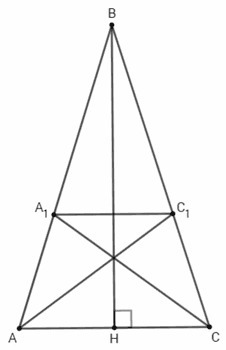
AB=BC=40; BH=4√91
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
AA1/A1B= AC/BC
C1C/BC1= AC/AB
AB=BC => AA1/A1B= C1C/BC1
Если прямые отсекают на секущих пропорциональные отрезки, то прямые параллельны.
AC||A1C1
△ABC~△A1BC1 (углы при основаниях равны как соответственные при AC||A1C1)
k= AC/A1C1 =AB/A1B
AH=√(AB^2 -BH^2) =√(1600 -16*91) =12
Высота в равнобедренном треугольнике является медианой.
AC=2AH =12*2 =24
AA1/A1B= AC/BC =24/40 =0,6
AB/A1B= (AA1 +A1B)/A1B =AA1/A1B +1 =1,6
A1C1= AC/k =24/1,6 =15