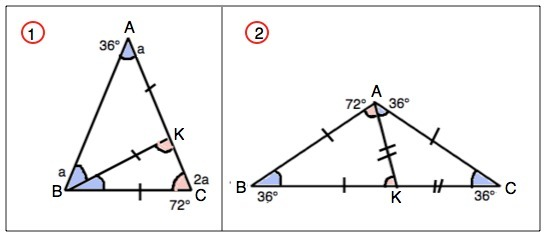
Задача имеет два решения.
1) Треугольник остроугольный. Обозначим прямую, которая делит исходный треугольник на два равнобедренных, ВК.
Треугольники АВС и КВС подобны, ∠ВКС=∠КСВ.
Примем ∠ВАК=∠АВК=а.
Угол ВКС - внешний угол треугольника АВК. Внешний угол равен сумме двух внутренних, не смежных с ним .⇒
Угол ВКС= 2а.
Тогда угол АСК=ВКС=2а, угол АВК=АСВ=2а.
Сумма углов ∆ АВС=5а=180°, откуда ВАС=а=36°. ∠В=∠С=72°
2) Равнобедренный треугольник ВАС тупоугольный.
Углы АВК=АСК. ∆ АКС подобен ∆ ВАС⇒∠КАС=∠АСК
Примем углы А и С равными а. ⇒
Угол АКВ - внешний для АКС и равен 2а, ∠ВАК=∠АКВ=2а
Тогда сумма углов ∆ ВАС=а+2а+а+а=5а ⇒
5а=180°. а=36°, откуда ∠В=∠С=36°, угол А=108°