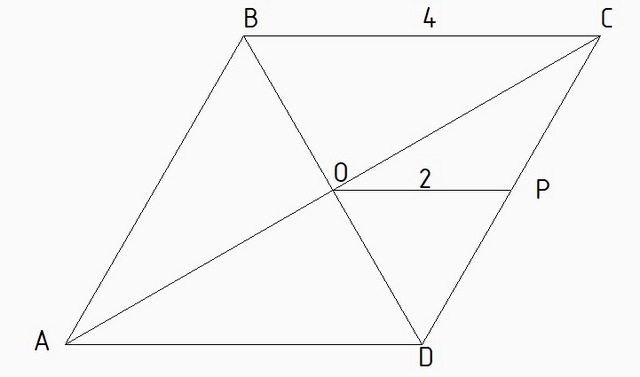
В ромбе сумма углов
BAD + ABC = 180
И один в два раза больше
BAD * 2 = ABC
---
BAD + BAD * 2 = 180
BAD * 3 = 180
BAD = 60°
ABC = 120°
Итак, угол С в треугольнике ВСД = 60 градусов. Как, впрочем и все остальные углы.
Отрезок ОР является средней линией треугольника ВСД - точка Р - медиана его стороны, точка О - пересечение диагоналей, которые в параллелограмме точкой пересечения делятся пополам.
Значит, сторона ВС в 2 раза длинне ОР, и равна 4 см
А так как треугольник ВСД равносторонний, то и диагональ ВД равна 4 см