Task/26566758
--------------------
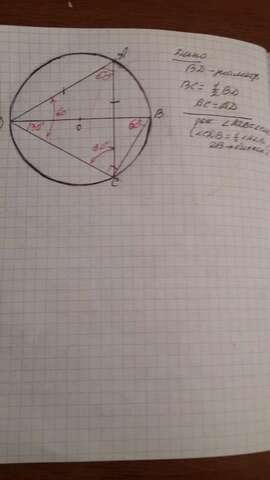
∠BCD = 90° (вписанные угол опирающий на диаметр BD).
BC = (1/2) *BD ⇒ ∠СDВ =30° (катет против угла 30° равен половине гипотенузы ) , значит ∠СBD =90° - ∠СDВ =90° - 30° =60 °.
∠CAD =∠СBD как вписанные углы опирающиеся на одну и ту же дугу СD.
∠CAD =60° , но треугольник CAD равнобедренный ,следовательно
∠ADC =∠ACD = 60°.
∠СDВ = 30° =60° /2 = (1/2)∠ADC .
т.е. DB биссектриса угла ADC , что и требовалось доказать .
не вредно для здоровья и просмотр ПРИЛОЖЕНИЕ