1
Периметр прямоугольника равен 44 см, а его стороны относятся как 4 к 7
пусть длина короткой стороны 4х, длинной 7х. Пеример
P = 2*(4x+7x) = 44
2*(4x+7x) = 44
4x+7x = 22
11х = 22
х = 2 см
короткая сторона 2*4 = 8 см
длинная сторона 2*7 = 14 см
2.
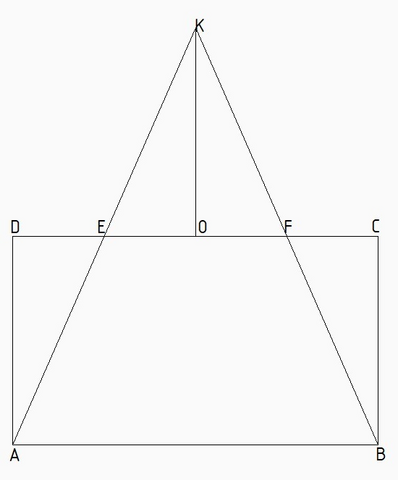
DE = FC = 1/2 EF
всё вместе равно 14 см, значит
DE = FC = 14/4 =3.5 см
EF = 14/2 = 7 см
Перпендикуляр из токи К к стороне DC точкой О делит EF пополам, EO = FO = 3.5 см
Треугольники ADE и KOE равны меж собой - у них все три угла одинаковых (один как вертикальные, другие как углы, образованные секущей параллельных прямых и накрест лежащие) и одна сторона равна, DE = EO.
Точно так же равны друг другу треугольники KOF и FCB
Из-за попарного равенства этих четырёх треугольников следует, что прямоугольник ABCD и треугольник АКВ равновелики друг другу.
Площадь прямоугольника 8*14 = 112 см²
Площадь треугольника такая же.