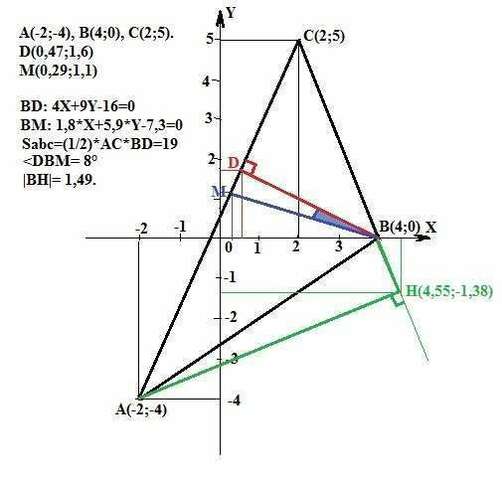
Даны вершины треугольника: А(-2;-4), В(4;0), С(2;5).
Найти а) уравнение высоты BD;
б) уравнение биссектрисы ВМ;
в) Sabc;
г) угол между BD и BM;
д) проекцию вектора АВ на ВС.
Решение:
а) Уравнение прямой АС, проходящей через данные точки А и С:
(X-Xa)/(Xc-Xa)=(Y-Ya)/(Yc-Ya) или
(X+2)/4=(Y+4)/9 - каноническое уравнение прямой АС =>
9X-4Y+2=0 (1) - общее уравнение прямой АС =>
Y=(9/4)*X+1/2 - уравнение прямой АС с угловым коэффициентом k1=9/4.
Условие перпендикулярности прямых AC и BD: k2=-1/k1.
Тогда k2=-4/9.
Точка В(4;0)
Уравнение прямой ВD, проходящей через точку В перпендикулярно прямой АС, находим по формуле:
Y-Yb=(-4/9)(X-Xb) или
Y=-(4/9)(X-4) отсюда общее уравнение высоты BD:
4X+9Y-16=0 (2).
Сразу найдем координаты точки D, решая систему уравнений (1) и (2):
Xd=46/97 ≈0,47.
Yd≈1,6.
Вектор BD{Xd-Xb;Yd-Yb} или BD{-3,5;1,6}.
Его модуль (длина): |BD|=√(Xdb²+Ydb²) или |BD|=√(12,25+2,56)=√14,81≈3,85.
б) Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон (свойство).
|BC|=√[(Xc-Xb)²+(Yc-Yb)²] или |BC|=√(4+25)=√29.
|BA|=√[(Xa-Xb)²+(Ya-Yb)²] или |BA|=√(36+16)=√52.
Значит точка М делит сторону СA в отношении k=√(29/52)≈0,75, считая от вершины С.
По формулам деления отрезка в данном отношении, найдём координаты точки М:
Xm=(Xc+0,75*Xa)/(1+0,75) = (2-0,75*2)/(1,75) ≈0,29.
Ym=(Yc+0,75)*Ya)/(1+0,75) = (5-0,75*4)/(1,75) ≈1,14.
Вектор ВМ{-3,71;1,14}.
Уравнение биссектрисы (прямой, проходящей через точки М и В):
1,14*X+3,71Y-4,56=0 (1).
Для определения уравнения биссектрисы угла между двумя прямыми, заданными общими уравнениями, есть специальная формула,
использующая то, что точки на биссектрисе равноудалены от сторон, образующих этот угол.
Каноническое уравнение прямой ВС: (X-4)/-2=(Y-0)/5.
Общее уравнение прямой ВС: 5X+2Y-20=0 c коэффициентами А1=5, В1=2, С1=-20.
Каноническое уравнение прямой ВА: (X-4)/-6=(Y-0)/-4.
Общее уравнение прямой ВА: 4X-6Y-16=0 c коэффициентами А2=4, В2=-6, С2=-16.
Тогда уравнение биссектрисы находим по формуле:
|(A1+B1+C1)/(√(A1+B1)| = |(A2+B2+C2)/(√(A2+B2)| - модуль в формуле означает, что можно получить два уравнения для биссектрис (взаимно перпендикулярных) внутреннего и внешнего углов между прямыми. В нашем случае:
(5x+2y-20)/√29 = (4X-6Y-16)/√52 или, взяв приближенные значения корней,
14,4*X+46,8*Y-57,6=0 или, разделив на 8:
1,8*X+5,85*Y-7,2=0 (2). Сравнивая уравнения (1) и (2), видим, что введя коэффициент 1,8/1,14 ≈1,6, мы получим из (1):
1,8*X+5,9*Y-7,3=0. С учетом погрешности при вычислениях видно, что уравнение биссектрисы найдено верно.
в) Для определения площади треугольника, заданного координатами вершин, так же есть специальная формула:
Sabc=|0,5[(Xa-Xc)(Yb-Yc)-(Xb-Xc)(Ya-Yc)]| (в ответе - модуль значения).
В нашем случае:
Sabc=|0,5[(-2-2)(0-5)-(4-2)(-4-5)]| = |0,5[20+18]| = 19 ед².
Или Sabc=(1/2)*AC*BD. В нашем случае
Sabc=(1/2)*9,85*3,85 ≈ 18,96 ≈19ед².
г) Угол между векторами вычисляется по формуле:
arccosα=(x1*x2+y1*y2)/[√(x1²+y1²)*√(x2²+y2²)]. В нашем случае угол между векторами BD и ВМ равен:
arccosα=(-3,5*(-3,71)+1,6*1,14)/[√(12,25+2,56)*√(13,76+1,3)] ≈ 14,8/15=0,99.
Тогда α ≈ 8°.
д) Общее уравнение прямой ВС: 5X+2Y-20=0, отсюда уравнение с угловым коэффициентом:
Y=(-5/2)X +10. k1=-5/2. Условие перпендикулярности прямых BC и AH: k2=-1/k1.
Тогда k2=2/5.
Точка A(-2;-4).
Уравнение прямой AH, перпендикулярной прямой BС, находим по формуле:
Y-Ya=(2/5)(X-Xa) или
Y+4=(2/5)(X+2) отсюда общее уравнение высоты AH:
2X-5Y-16=0.
Сразу найдем координаты точки Н, решая систему уравнений:
5X+2Y-20=0 и 2X-5Y-16=0.
Xh=132/29 ≈4,55.
Yh≈-1,38.
Тогда проекция АВ на ВС - это катет ВН.
|ВН|=√[(Xh-Xb)²+(Yh-Yb)²] или |BC|=√(0,55²+(-1,38)²) ≈√2,21 =1,49.