Найти площадь ромба если разница между диагоналями 5 и длина вписаной окружности 12п

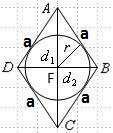
Нам нужно найти S=(d₁*d₂)/2
пусть диагонали d₁ и d₂
по условию
d₁-d₂=5
R-это высота в прямоугольном ΔABF
⇒
$R= \frac{AF*BF}{ \sqrt{AF^{2} +BF^{2} } }$
R=(d₁*d₂)/(2√(d₁²+d₂²))
L-длина окр
L=2πR=2π(d₁*d₂)/√(2(d₁²+d₂²))=12π
(d₁*d₂)/√(d₁²+d₂²)=12
d₁*d₂=12√(d₁²+d₂²)
возведем в квадрат
d₁² * d₂²=144(d₁²+d₂²)
d₁²+d₂²=d₁²*d₂²/144

d₁-d₂=5
d₁²+d₂²=25+2d₁d₂

d₁²*d₂²/144 = 25+2d₁d₂
пусть d₁d₂=t
t²/144=25+2t
t²-288t-3600=0
D₁=144²+3600=144²+60²=24336=156²
t=144±√24336
t=144±156
т.к. диагонали положительны то
t=300
S=t/2=150 ед²