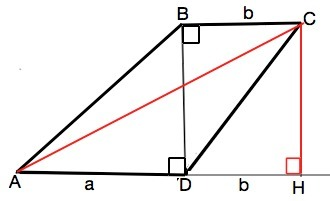
Треугольники АВD и СВD прямоугольные.
Сумма острых углов прямоугольного треугольника 90°
∠ВАD+∠ABD=90°
∠ВАD+∠ВСD=90° по условию ⇒
∠АВD=∠BCD.
Если в прямоугольных треугольниках равен один из острых углов. эти треугольники подобны.
∆ АВD~∆ CBD ⇒
BC:BD=BD:AD⇒
BD² =AD•BC=a•b
Опустим из С перпендикуляр до пересечения с продолжением АD в точке Н.
СН=ВD
СН²=BD²=ab
Из ∆ АСН по т.Пифагора
АС²=АН²+СН²
АС²=(а+b)²+ab
AC²=a²+2ab+b²+ab=a²+3ab+b²
AC=√(a²+3ab+b²)