Помогите пожалуйста, я в отчаянии,

ДАНО

Y = (x²-21)/(x-2)

1.Область определения D(x). х-2≠0. х≠2 - разрыв функции.

Х∈(-∞;2)∪(2;+∞). Вертикальная асимптота Х= 2.

2. Пересечение с осью Х. Y=0. Действительных решений нет.

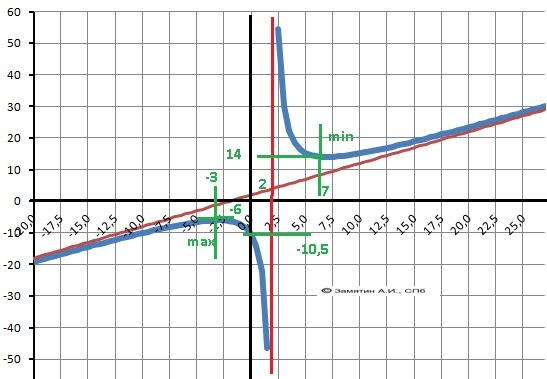
3. Пересечение с осью У. У(0) = -21/2 = - 10,5 .

4. Поведение на бесконечности.limY(-∞) = - ∞, limY(+∞) = +∞

Поведение в точке разрыва. lim(2-) =-∞, lim(2+)=+∞.

5. Исследование на чётность.Y(-x) = (x²-21)/(-х-2) ≠ Y(x).

Функция ни чётная ни нечётная.

6. Производная функции.

$Y'(x)= \frac{21-4x+x^2}{(x-2)^2}= \frac{(x-7)(x+3)}{(x-2)^2}=0$

Корни при Х=-3 и Х=7. Схема знаков производной.

_ (-∞)__(>0)__(-3)___(<0)___(7)__(<0)_____(+∞)__</p>

7. Локальные экстремумы. Максимум Ymax(-3)= -6, минимум – Ymin(7)=14. 8. Интервалы возрастания и убывания.

Возрастает - Х∈(-∞;-3)∪(7;+∞) , убывает = Х∈(-3;2)∪ (2;7).

8. Вторая производная - Y"(x)=0 при Х=2 - в точке разрыва.

Точка перегиба Х= 2.

9. Выпуклая “горка» Х∈(-∞;2), Вогнутая – «ложка» Х∈(2;+∞).

10. Область значений Е(у) У∈(-∞;+∞)

11. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).

$k= \lim_{x \to \infty} \frac{x+ \frac{21}{x} }{1- \frac{2}{x} }=x$

. b = lim(∞)Y(x) – k*x=2

12. График в приложении.