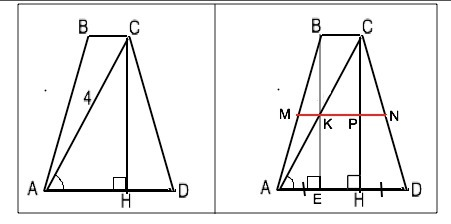
Сделаем рисунок. Обозначим вершины трапеции АВСД.
Опустим из вершины С тупого угла высоту СН.
Способ 1)
По свойству высоты равнобедренной трапеции, опущенной из вершины тупого угла, она делит основание на отрезки, бóльший из которых равен полусумме оснований, меньший - их полуразности.
Диагональ, высота и бóльший отрезок основания образуют прямоугольный треугольник АСН с углом САН=60°.
Т.к сумма острых углов прямоугольного треугольника 90°, ∠АСН=30°
Катет АН противолежит этому углу и по свойству такого катета равен половине гипотенузы.
Гипотенуза=диагональ = 4.
АН=4:2=2см
АН – полусумма оснований, т.е. она равна средней линии трапеции, Это ответ.