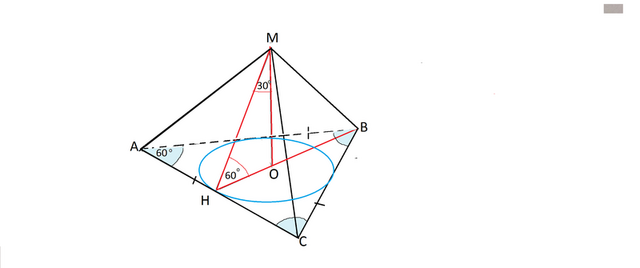
Высота правильной треугольной пирамиды равна 4√3, а боковая грань образует с основанием пирамиды угол 60° .Найдите площадь боковой поверхности.
----------------
Площадь боковой поверхности пирамиды равна сумме площадей ее граней или половине произведения апофемы на периметр основания пирамиды.
Апофема МН равна частному от деления высоты пирамиды на синус угла МНО.
МН=((4√3):(√3:2)=8
НО - треть высоты основания пирамиды, т.к. равен радиусу вписанной в правильный треугольник окружности, т.е. одной трети высоты этого треугольника.
ОН противолежит углу НМО= 30° ⇒ равна половине МН.
ОН=МН:2=4
Вся высота ВН равна 4×3=12
Сторона основания АВС равна
НВ :sin 60°=8√3
Площадь боковой поверхности пирамиды
S бок=Р АВС×МН
:2= 24√3×8
:2=
96√3 единиц площади