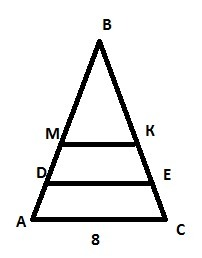
Дано:
МК-средняя линия,
АD=DM, EC=KE
АС=8 cм
АМКС-?
DE-?
Решение.
МК-средняя линия по условию⇒ МК║АС. Геометрическая фигура, у которой 2 стороны параллельны, а 2 нет является трапецией, значит АМКС-трапеция.
АМ=МВ, ВК=КС-по условию, так как МК-средняя линия ΔАВС. Значит МК=1/2АС, МК=1/2*8=4см.
AD=MD KE=EC, значит DE║MK║AC, DE- средняя линия трапеции. ⇒DE=(MK+AC)/2
DE=(4+8)/2=6см.
Ответ: АМКС-трапеция, DE=6см