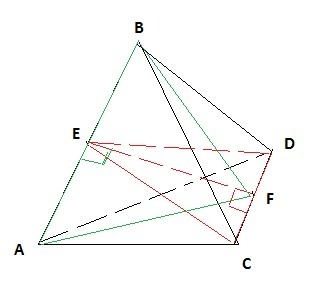
Тетраэдр-пирамида, у которой все грани-правильные треугольники.
Рассмотрим ΔDEC:
DE=EC, так как Е-середина АВ по условию,
DF=FC, так как F-середина стороны DC по условию.
ЕF-медиана равностороннего ΔDEC, а значит и высота⇒EF⊥DC.
Рассмотрим ΔAFB:
AF=FB, так как F-середина стороны DC по условию.
AE=EB, так как Е-середина АВ по условию,
ЕF-медиана равностороннего ΔAFB, а значит и высота⇒EF⊥AB
Если АВ=4см, то в ΔAFB EF=√(AF²-AE²)
EF=√(16-4)=√12=2√3 см