Окружности с центрами в точках M и N пересекаются в точках S и T,причём точки M и N лежат...

Question

Окружности с центрами в точках M и N пересекаются в точках S и T,причём точки M и N лежат по одну сторону от прямой ST.Докажите что прямые MN и ST перпендикулярны.

Answer 1

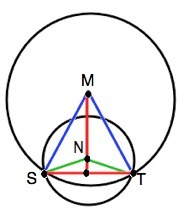
Концы хорды  ST лежат на обеих окружностях. 

Треугольники SMT и  SNT равнобедренные, так как их боковые стороны - радиусы соответственно большей и меньшей окружностей. 

В ∆ SMN и ∆ TMN стороны SM=MT; SN=NТ.  MN- общая. Эти треугольники равны по 3-м сторонам. 

Тогда ∠SМN=∠TMN, ⇒ MN- биссектриса угла SMT. В равнобедренном треугольнике биссектриса является ещё и медианой и высотой. Следовательно, MN и ST перпендикулярны.

---