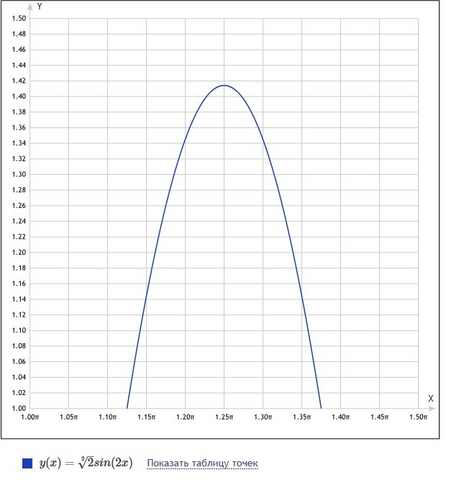
f(x)=sin2x/(√2/2)=√2*sin2x
f`(x)=√2*cos2x*2
f`(x)=0; cos2x=0; 2x=pi/2+pik; x=pi/4+pik/2
f(pi/4)=√2*sin(pi/2)=√2
f(pi)=√2*sin(2pi)=0
f(3pi/2)=√2*sin(3pi)=0
вообще f(min)= √2*sin2x=√2*(-1)=-√2 при x=3pi/4
но это 135 градусов в указанный интервал не входит
поэтому минимум на указанном промежутке на концах интервала и равен 1