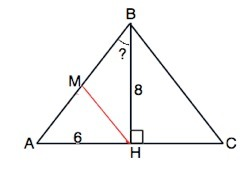
Для решения нарисуем осевое сечение конуса – равнобедренный треугольник АВС. Радиус АН=6 см. Высота ВН=8 см. НМ - расстояние от центра основания до середины образующей.
∆ АВН прямоугольный.
По т.Пифагора АВ=10 см (можно не высчитывать, обратив внимание на отношение катетов 3:4 - это "египетский" треугольник)
а) синус угла между образующей АВ и высотой ВН - отношение противолежащего катета АН к гипотенузе АВ.
sin∠АВН=6:10=0,6 ⇒ Угол АВН=arctg 0,6 или 36°52'
б) М - середина гипотенузы прямоугольного треугольника. ⇒
НМ - медиана. По свойству медианы прямоугольного треугольника, проведенной к гипотенузе, её длина равна половине длины гипотенузы.
НМ=АВ:2=10:2=5 см