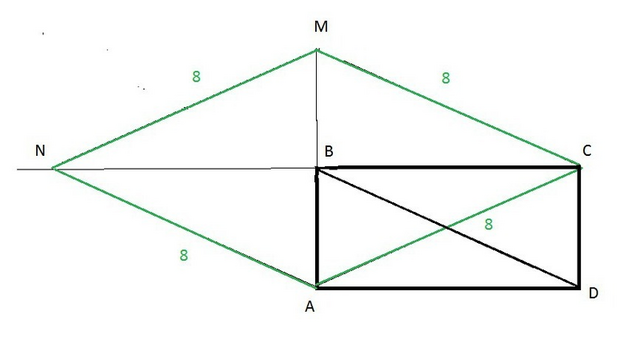
Диагонали прямоугольника равны
АС=BD=8 cм.
СМ ║ BD
BM ║ CD
BDCM - параллелограмм, значит MC=BD=8 cм
MN ║ AC
∠MNB = ∠BCA-внутренние накрест лежащие углы при параллельных прямых MN и АС и секущей NC.
АВ=СD=BM ⇒ AB=BM
ΔBMC =ΔABC по катету и острому углу.
Из равенства треугольников следует равенство сторон
MN=AC=8 cм
ΔMNB = Δ ANB по двум катетам.
NB- общий катет;
АВ=ВМ
Значит MN=NA=8 cм
Р( АCMN)=AC+CM+MN+NA=8+8+8+8=32 cм.