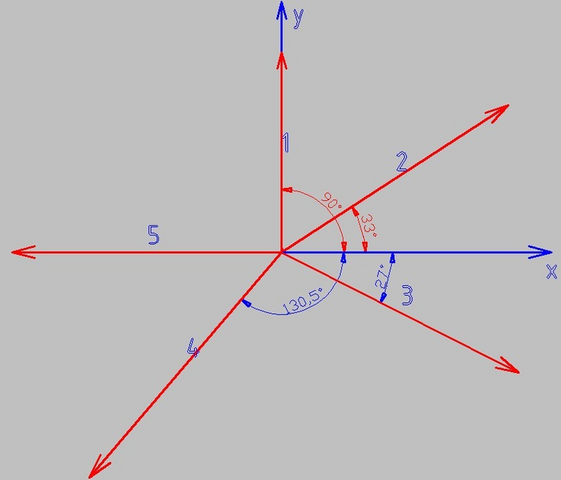
Можно разложить векторы по компонентам x и y и просуммировать
x₁ = 52*cos(90°)
x₂ = 70*cos(33°)
x₃ = 69*cos(-27°)
x₄ = 77*cos(-130,5°)
x₅ = 70*cos(-180°)
x = x₁+x₂+x₃+x₄+x₅ = 52*cos(90°)+70*cos(33°)+69*cos(-27°)+77*cos(-130,5°)+70*cos(-180°) = 0,18
y₁ = 52*sin(90°)
y₂ = 70*sin(33°)
y₃ = 69*sin(-27°)
y₄ = 77*sin(-130,5°)
y₅ = 70*sin(-180°)
y = 52*sin(90°)+70*sin(33°) +69*sin(-27°) +77*sin(-130,5°) +70*sin(-180°) = 0,25
Модуль равнодействующей
r = √(x²+y²) = √(0,18²+0,25²) = 0,308
и угол с осью X
tg(α) = y/x = 0,25/0,18 = 54,25°
По сравнению с величиной самих сил равнодействующая можно сказать нулевая.