Находим производную заданной функции.
 .
.
Из этого выражения видны свойства функции.
Аргумент функции не имеет отрицательных значений.
Имеется точка разрыва функции: х = 0.
Находим экстремум, приравняв производную нулю (достаточно числитель): 3(х³ - 1) = 0.
Получаем одно значение: х = 1 и два промежутка области определения функции: (0; 1) и (1; ∞).
Определяем знаки производной.
На
промежутках находим знаки производной. Где
производная положительна - функция возрастает, где отрицательна - там убывает.
Точки, в которых происходит смена знака и есть точки экстремума - где
производная с плюса меняется на минус - точка максимума, а где с минуса на плюс
- точки минимума.
x = 0,5 1 2
y' = -5,25 0 10,5 .
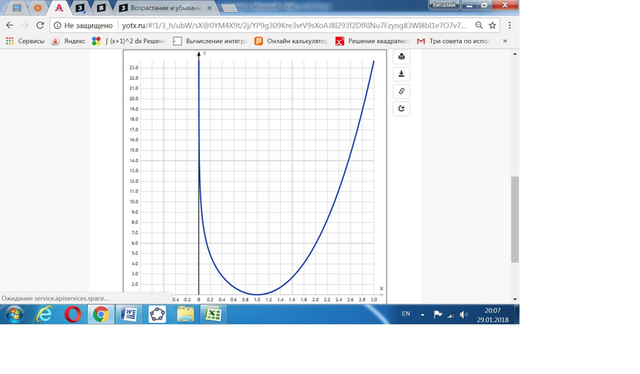
Отсюда видим, что минимум функции при х = 1.
Значит, на промежутке х ∈ (0; 1) функция убывающая,
на промежутке х ∈ (1; ∞) функция возрастающая.