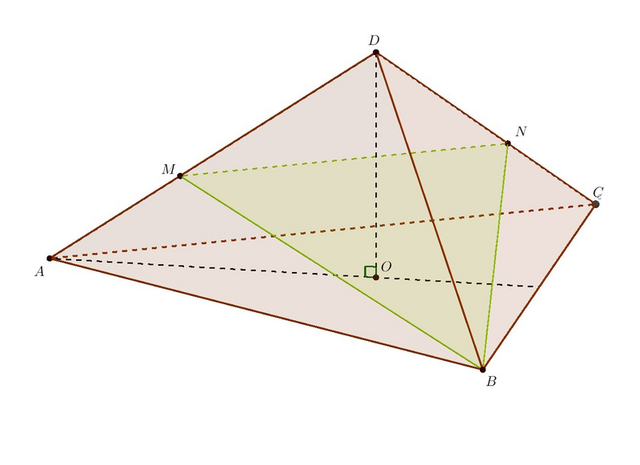
А) Проведём высоту DO и прямую AO. Пирамида будет правильной, если O — центр треугольника ABC.
AD по условию перпендикулярна DB и DC, значит, перепендикулярна плоскости (DBC), а значит, и прямой BC, лежащей в этой плоскости.
DO по построению перпендикулярно плоскости (ABC), значит, и прямой BC, лежащей в этой плоскости.
BC перпендикулярна AD и DO, поэтому перпендикулярна плоскости (ADO) и прямой AO ∈ (ADO). Значит, на прямой AO лежит высота треугольника ABC. Аналогично, и на BO лежит высота треугольника ABC. Так как высоты правильного треугольника пересекаются в центре, то O — центр треугольника, а пирамида — правильная.
б) Пирамида правильная, значит, все боковые стороны равны, боковые грани —равнобедренные прямоугольные треугольники.
DA = DB = DC = AC * sin(45°) = 5√2.
Рассмотрим треугольники ADC и MDN. Они подобные (угол D общий, MD : AD = ND : CD = 3 : 5) с коэффициентом подобия 3/5, тогда MN = 3/5 * AC = 6.
Рассмотрим треугольник DMB. Он прямоугольный с прямым углом D, DM = 3/5 AD = 3√2, DB = 5√2. По теореме Пифагора MB = √(DM^2 + DB^2) = √2 * √(3^2 + 5^2) = 2√17. Аналогично, BN = 2√17.
Треугольник BMN — равнобедренный с основанием MN = 6 и боковыми рёбрами MB = BN = 2√17. Проведём в нём высоту BX. BX — также медиана, значит, XN = MN/2 = 3.
По теореме Пифагора для треугольника BXN
BX = √(BN^2 - XN^2) = √(68 - 9) = √59
Тогда площадь треугольника BMN = 1/2 * BX * MN = 3√59.