Формула площади треугольника
Ѕ=а•h/2
а=12 по условию. Высоту нужно найти.
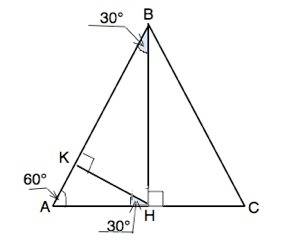
Опустим высоту ВН треугольника АВС. В равностороннем треугольнике высота еще медиана и биссектриса ⇒
АН=12:2=6,
∠АВН=30°
∆ АВН - прямоугольный.
Проведем его высоту НК.
Сумма острых углов прямоугольного треугольника 90°⇒
∠КНА=90°- 60°=30°
Катет АК противолежит углу 30° и равен АН:2= 6:2=3
Тогда КВ=12-3=9
Треугольники АВН и НВК подобны по равному острому углу 30°.
Из подобия следует ВК:КН=КН:АК ⇒
КН²=АК*КВ=3°9=27 ⇒
КН=3√3
Гипотенуза ВН треугольника КВН=2•КН=6√3.
S (ABC)=BH•AC/2=(6√3)•12/2=36√3= ≈62,354 ед. площади.