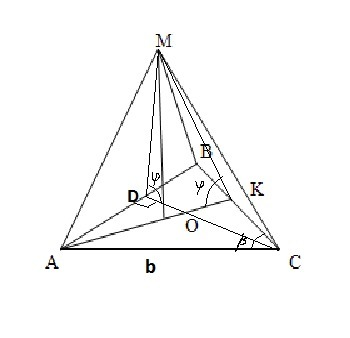
Осталось найти боковую площадь.Она состоит из 2 равных равнобедренных треугольника с основанием b и еще одного равнобедренного с основанием ВС.
Основанием высоты пирамиды будет точка О, которая является центром вписанной окружности в ΔАВС,надо вычислить этот радиус-чтобы потом через него вычислить высоты боковых граней.
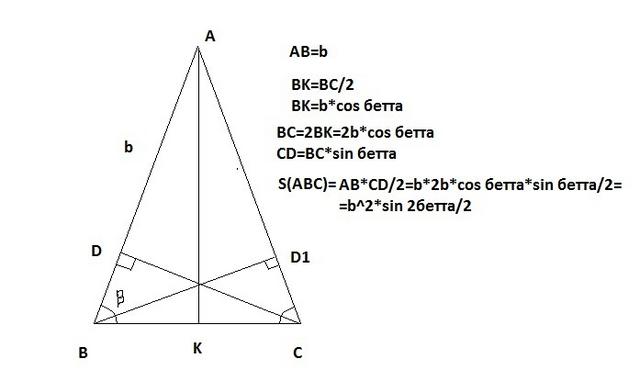
r=(BC/2)√((2b-BC)/(2b+BC))=b*cosβ*√((1-cosβ)/(1+cosβ))(вычисления я опустила)
Тогда высота боковых граней будет
KM=r/cosФ=b*cosβ*√((1-cosβ)/(1+cosβ))/cosФ
S(бок)=(b+b+BC)*KM/2=(2b+2b*cosβ)*b*cosβ*√((1-cosβ)/(1+cosβ))/2cosФ=
=(1+cosβ)*b^2*cosβ*√((1-cosβ)/(1+cosβ))/cosФ
S(пол)=S(осн)+S(бок)=b^2*sin2β/2+(1+cosβ)*b^2*cosβ*√((1-cosβ)/(1+cosβ))/cosФ