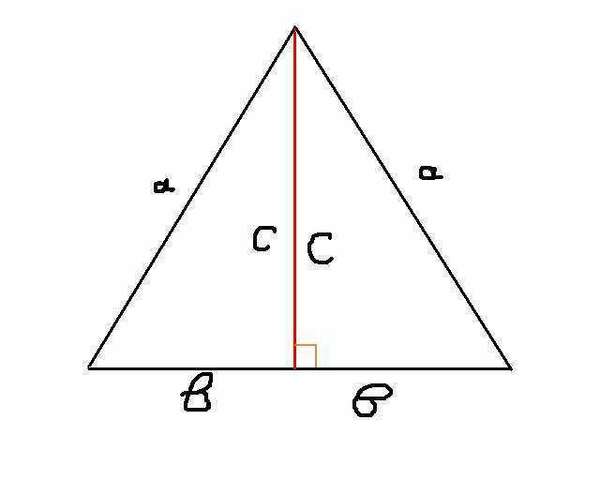
Медиана - отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны. То есть: получаем два прямоугольных (это получается от того, что медиана стоит перпендикулярно) треугольника, разрезанных медианой с равной длиной катетов (один - потому, что медиана делит на два равных отрезка; второй - сама медиана, общая для обоих). Гипотенузы, соответственно, тоже будут одинаковой длины.
Как-то, блин, путанно... но не знаю, как ещё...
картинка: