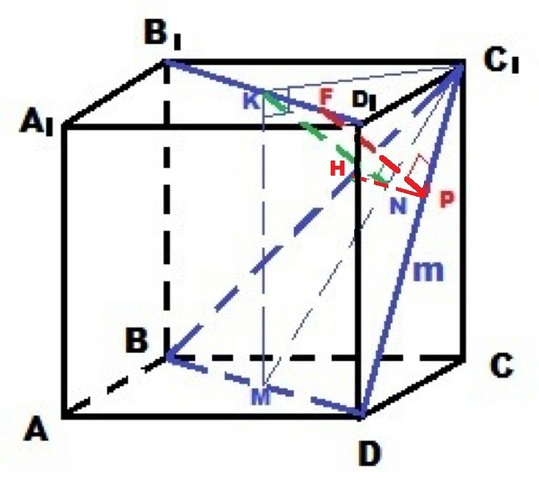
BD║B₁D₁ как диагонали параллельных граней куба.
BD лежит в плоскости BDС₁ ⇒ B₁D₁║(BDС₁) - по теореме "Если прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в плоскости, то эта прямая параллельна и самой плоскости"
ΔMKC₁ : построить высоту KN⊥MC₁
Через точку N в плоскости BDС₁ провести прямую HP║B₁D₁. Следствие из аксиом стереометрии "Через две параллельные прямые можно провести плоскость и только одну" ⇒ в плоскости KHP лежат обе параллельные прямые HP║B₁D₁
Так как по построению KN⊥MC₁, KN∈(KHP), MC₁∈(BDC₁) ⇒
плоскость KHP перпендикулярна плоскости BDC₁
Точка P лежит на прямой DC₁. Перпендикуляр из точки P будет лежать в плоскости KHP:
PF⊥DC₁ и PF⊥HP ⇒
так как HP║B₁D₁, то PF⊥B₁D₁ по теореме "если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй параллельной прямой" ⇒
Расстоянием между скрещивающимися прямыми является длина их общего перпендикуляра. Так как PF⊥DC₁ и PF⊥B₁D₁, то отрезок PF и есть расстояние между прямыми DC₁ и B₁D₁
Так как прямая B₁D₁ параллельна плоскости BDС₁, KN⊥(BDC₁), PF⊥(BDC₁) ⇒
KN = PF как два перпендикуляра между плоскостью и прямой, которая параллельна плоскости ⇒
KN = PF - расстояние между скрещивающимися прямыми DC₁ и B₁D₁