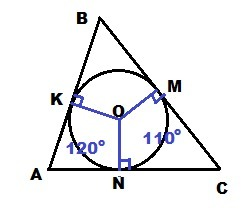
Так как рисунок с расположением точек K, M, N отсутствует,
пусть K∈AB; M∈BC; N∈AC.
Радиусы в точку касания образуют прямые углы с касательными:
OK⊥AB; OM⊥BC; ON⊥AC
Градусная мера дуги окружности равна градусной мере центрального угла, который опирается на эту дугу. ⇒
∠MON = ∪MN = 110°
∠KON = ∪KN = 120°
Сумма углов четырехугольника
(n - 2)*180°=(4 - 2)*180° = 2*180° = 360°
Четырехугольник CMON.
∠С = 360° - ∠ONC - ∠OMC - ∠MON =
= 360° - 90° - 90° - 110°= 70°
Четырехугольник AKON.
∠A = 360° - ∠OKA - ∠ONA - ∠KON =
= 360° - 90° - 90° - 120°= 60°
ΔABC: ∠B = 180° - ∠A - ∠C = 180° - 70° - 60° = 50°
Ответ: углы треугольника 50°, 60°, 70°