Используем вид записи  для поиска переменных, используемых для вычисления амплитуды, периода, сдвига по фазе и вертикального сдвига.
для поиска переменных, используемых для вычисления амплитуды, периода, сдвига по фазе и вертикального сдвига.




Найдем амплитуду  .
.
Амплитуда: 1
Определим период при помощи формулы  .
.
Период: 
Подставим 1 вместо  в формуле для периода.
в формуле для периода.
Период: 
Решим уравнение.
Модуль - это расстояние между числом и нулем. Расстояние между 0 и 1, равно 1:
Период: 
Делим  на 1, получаем
на 1, получаем  .
.
Период: 
Найдем сдвиг периода при помощи формулы  .
.
Фазовый сдвиг функции можно вычислить с помощью  :
:
Фазовый сдвиг: 
Заменим величины  и
и  в уравнении для фазового сдвига:
в уравнении для фазового сдвига:
Фазовый сдвиг: 
Умножим числитель  на величину, обратную знаменателю 1:
на величину, обратную знаменателю 1:
Фазовый сдвиг: 
Умножив -1 на 1, получим -1:
Фазовый сдвиг: 
Найдем вертикальное смещение  :
:
Вертикальный сдвиг: 0
Перечислим свойства тригонометрической функции.
Амплитуда: 1
Период: 
Фазовый сдвиг:  (на
(на  влево)
влево)
Вертикальный сдвиг: 0
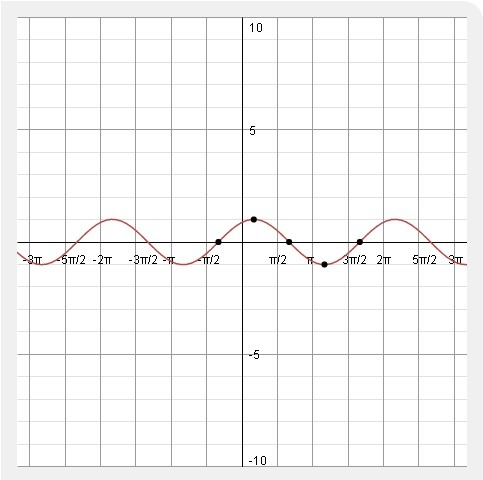
Выберем несколько точек для нанесения на график.
Найдем точку при  .
.
Заменим в выражении переменную  на
на  :
:

Упростим результат:
0
Найдем точку при  .
.
Заменим в выражении переменную  на
на  :
:

Упростим результат:
1
Найдем точку при  .
.
Заменим в выражении переменную  на
на  :
:

Упростим результат:
0
Найдем точку при  .
.
Заменим в выражении переменную  на
на  :
:

Упростим результат:
0
Перечислим точки на таблице, которая сейчас в разделе картинок.
Тригонометрическую функцию можно изобразить на графике, опираясь на амплитуду, период, фазовый сдвиг, вертикальный сдвиг и точки.
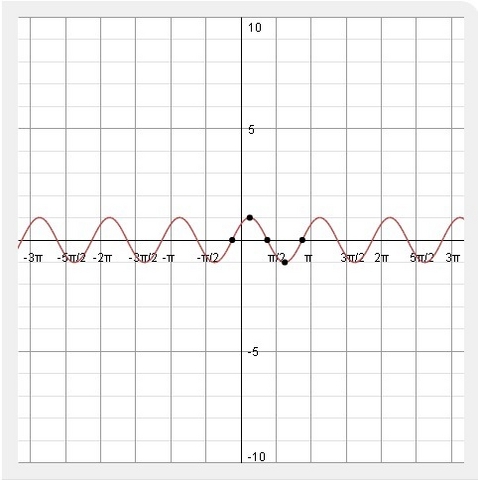
Со вторым все тоже самое.




Амплитуда: 1
Период: 
Фазовый сдвиг: 
Вертикальный сдвиг: 0
Фазовый сдвиг:  (на
(на  влево)
влево)