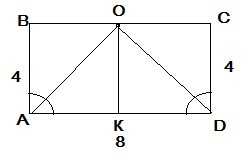
Площадь данного прямоугольника делится биссектрисами углов основания на 3 части.
∠ВАО=45°, так как АО-биссектриса угла⇒∠ВОА=90-45=45°⇒ВО=АВ=4см∠ODC=∠DOC=45°⇒OC=CD=4см.Опустим ОК⊥AD АК=ОВ=KD=OC=ОК=4 см Sтр АВО=Sтр ОСD=1/2*4*4=8см².
Sтр AOD=1/2*4*8=16cм²⇒биссектриса углов основания делит данный прямоугольник на 3 части: 8см², 8см²,16см²