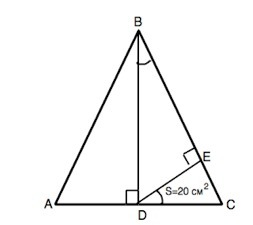
Медиана равнобедренного треугольника является и высотой.⇒
∆ BDC– прямоугольный.
Т.к. DC⊥ВС, то DE - высота прямоугольного треугольника и делит его на подобные
∆ ВЕD~∆ CED ( т.к. каждый из них подобен исходному ∆ BDC по общему острому углу:
угол В для ∆ BDC и ∆ BDE и угол С для ∆ BDC и ∆ CED)
Следовательно, по отношению гипотенуз ∆ ВЕD и ∆ CED коэффициент подобия k=2.
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
S(BDE):S(CDE)=k²=4
S(BDE)=4•S(CED)=4•20=80 см²⇒
S(BDC)=S(BED)+S(CDE)=80+20=100 см²
Медиана треугольника делит его на два равновеликих
S(ABD)=S(BDC)⇒
S(ABC)=S(BDC•2=100•2=200 см²