1)
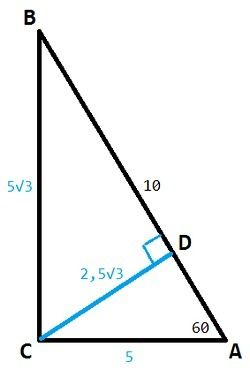
a) В треугольнике с углами 30°, 60°, 90° стороны относятся как 1:√3:2
В данном случае гипотенуза AB=10 см, множитель 5: AC=5 см, BC=5√3 см
б) △ACD~△ABC (по двум углам, прямоугольный, общий угол A).
k=AC/AB=1/2
CD=BC* 1/2 =5√3/2 =2,5√3 (см)
2)
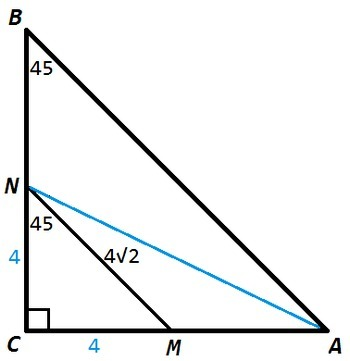
MN - средняя линия в △ABC (параллельна основанию, равна его половине)
AB=2MN =2*4√2 =8√2 (см)
AB||MN => ∠ABC=∠MNC=45° (соответственные углы)
a) В треугольнике с углами 45°, 45°, 90° стороны относятся как 1:1:√2
В данном случае гипотенуза AB=8√2 см, множитель 8: AC=8 см, BC=8 см
CN=BC/2 =8/2 =4 (см)
AN=√(AC^2+CN^2) =√(8^2 +4^2) =4√(4+1) =4√5 (см)
б) CM=CN=4 (△CNM - с углами 45°, 90°)
S(CMN)=CM*CN/2 =8 (см^2)
Средняя линия треугольника отсекает четверть площади
S(ABC)=4*S(CMN)
S(MABN)= 3*S(CMN) =8*3 =24 (см^2)