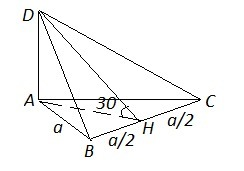
АН⊥ВС, АН - высота, медиана и биссектриса равностороннего ΔАВС.
AH=√(AB²-BH²)=√a²-(a/2)²)=a√3/2 .
Соединим D и Н. DH - наклонная к пл. АВС.
DA⊥ пл.АВС ⇒ DА ⊥ любой прямой в пл. АВС , DА⊥AH, АН - проекция DH на пл. АВС. Но проекция АН ⊥ВС ⇒ по теореме о трёх перпендикулярах DH⊥BC.
Тогда двугранный угол между плоскостями АВС и DBC - это ∠DHA=30°.
ΔDAH - прямоугольный. DA/AH=tg∠DHA , DA=AH*tg30°=a√3/2*√3/3=a/2.
AH/DH=cos30° ⇒ DH=AH/cos30°=a√3/2:√3/2=a
S(бок)=S(ABD)+S(ADC)+S(BCD)=1/2*AB*DA+1/2*AC*DA+1/2*BC*DH=
=1/2*(a*a/2+a*a/2+a*a)=1/2*2a²=a²