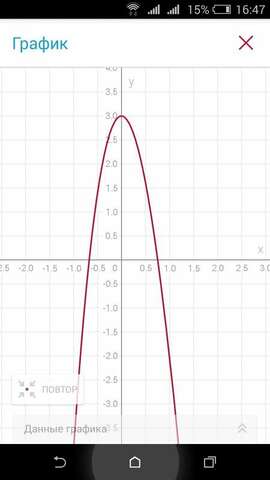
Строим график и видим: максимум: 3, минимум при -2 или при 2, подстановкой видим минимум при -2, он равен -29.
Альтернативное решение заключается в нахождении экстремумов функции при помощи производных и рассматривании двух участков.
Производную приравниваем к 0 для нахождения экстремумов кубической параболы:
3х^2-12х=0
х1=0 у1=0. А(0;0)
х2=-4 у2=-157. В(-4;-157)
На участке от -2 до 0:
производная больше 0, функция возрастает.
На участке от 0 до 2:
производная меньше 0, функция убывает.
Максимум при х=0 и у=3
Минимум либо при х=-2, либо при х=2. Подстановкой убеждаемся: минимум при х=-2, он равен -29.
Этот способ позволяет построить график, который указан выше, но построение графика при этом аналитическом способе не необходимо.