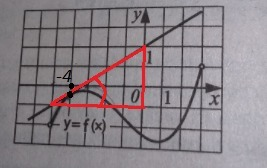
Если мы знаем уравнение касательной у=kx+b , то угловой коэффициент
k=y'(x₀) , где х₀ - абсцисса точки касания. Ещё известно , что y'(x₀)=tga .
Значит, для ответа на вопрос задачи, надо вычислить tg угла наклона касательной к положительному направлению оси ОХ ( угла "а").
Для этого нарисуем прямоугольный треугольник, где сама касательная будет гипотенузой, а катетами - прямые, параллельные осям координат, причём катеты должны проходить через узловые точки на чертеже (чтобы удобно было вычислять их длины). Отношение длины противолежащего катета к длине прилежащего катета даст tga.
tga=3/5 ⇒ y'(x₀)=y'(-4)=tga=3/5