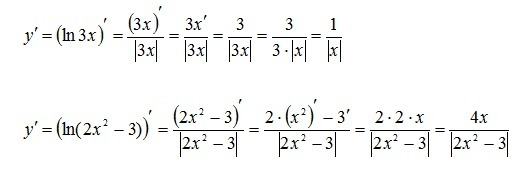Здесь в задаче 52 в обоих примерах нужно найти производную натурального логарифма с составным аргументом. Так что понадобятся два правила:
1) производная натурального алгоритма (lnx)'=1/|x|, здесь в знаменателе модуль аргумента
2) производная составной функции вычисляется по формуле:
(f(g(x)))'=f'(g(x))*g'(x), т.е. нужно найти производную внешней функции, умножить на производную составного аргумента и т.д.
Т.е., например, ln'(3x)=1/|3x|*(3x)'=1/|3x|*3*x'=1/|3x|*3=3/|3x|=1/|x|
Остальные правила - стандартные правила нахождения производной:
3) производная константы равна 0
4) производная аргумента х равна 1
и т.д.
Подробное решение - на рисунках...