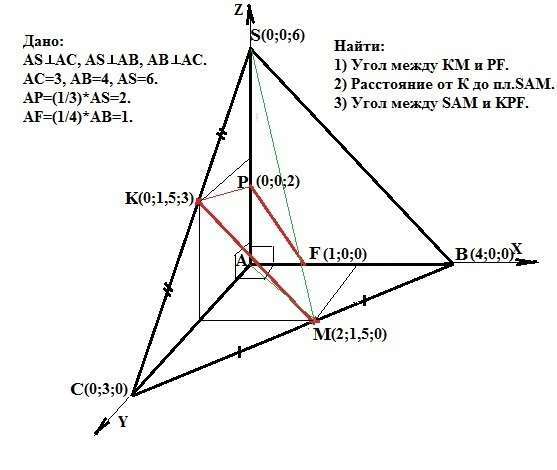
Дано: SABC - пирамида.
AS⊥AC, AS⊥AB, AB⊥AC.
АС=3, АВ=4, АS=6.
АР=(1/3)*AS=2.
AF=(1/4)*AB=1.
Найти:
1) Угол между прямыми КМ и РF.
2) Расстояние от К до пл.SAM.
3) Угол между плоскостями SAM и KPF.
Решение.
Привяжкм систему кородинат к вершине А(0;0;0).
Тогда имеем точки с координатами:
A(0;0;0), B(4;0;0), C(0;3;0), S(0;0;6),
P(0;0;2), F(1;0;0), K(0;1,5;3), M(2;1,5;0).
1). Угол α между вектором a и b:
cosα=(x1*x2+y1*y2+z1*z2)/[√(x1²+y1²+z1²)*√(x2²+y2²+z2²)].
В нашем случае вектор КМ={2;0;-3}, |KM|=√(4+0+9)=√13
и вектор PF={1;0;-2}, |PF|=√(1+0+4)=√5.
Cos(KM^PF)=(2*1+0*0+(-3)*(-2))/(√13*√5) ≈ 8/8,06 ≈ 0,9926.
Искомый угол равен arccos(0,9926) ≈ 7° (по таблице).
2. Расстояние от точки K до плоскости SAM находится по формуле:
d = |A*Xk+B*Yk+C*Zk+D|/√(A²+B²+C²), где А,В,С и D - коэффициенты общего уравнения плоскости SAM.
Уравнение плоскости SAM найдем по формуле:
|x - xA xS - xA xM - xA|
|y - yA yS - yA yM - yA| = 0.
|z - zA zS - zA zM - zA|
Подставим данные трех наших точек:
|x 0 2 |
|y 0 1,5| = 0.
|z 6 0 |
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|0 1,5| |0 2| |0 2 |
(х)*|6 0 | - (y)*|6 0| +(z)*|0 1,5| =0.
x(-9)-y(-12)+Z(0)=0. Или 9x-12y-0z+0=0 Это общее уравнение плоскости с коэффициентами: A=9, B=-12, C=0 и D=0.
Тогда искомое расстояние от точки К до плоскости SAM равно:
d=|0*0+(-12)*1,5+0*3+0|/√(81+144+0) = 18/15 = 1,2.
3. Угол между плоскостями, заданными общими уравнениями, находится по формуле:
cosα=(A1*A2+B1*B2+C1*C2)/[√(A1²+B1²+C1²)*√(A2²+B2²+C2²)].
Уравнение плоскости SAM уже найдено.
Найдем уравнение плоскости KPF.
Подставим данные трех наших точек K(0;1,5;3), P(0;0;2) и F(1;0;0):
|x-1 -1 -1 |
|y-0 1,5 0 | = 0.
|z-0 3 2 |
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|1,5 0| |-1 -1| |-1 -1|
(х-1)*|3 2| - (y)*| 3 2| +(z)*|1,5 0| =0.
(x-1)*3-y(-2+3)+Z(1,5)=0. Или 3x-y+1,5z-3=0 Это общее уравнение плоскости с коэффициентами: A=3, B=-1, C=1,5 и D=-3.
Тогда искомый угол между плоскостями SAM и KPF равно:
cosα=(9*3+(-12*-1)+0*1,5)/[15*√(9+1+2,25)] = 39/52,5 ≈0,743.
Искомый угол равен arccos(0,743) ≈ 42°.