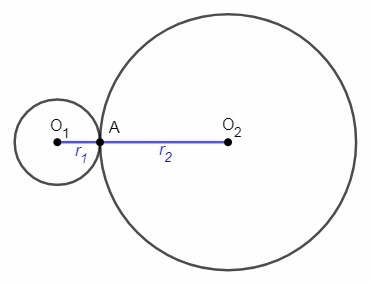
Точка касания двух окружностей (A) лежит на прямой, соединяющей центры (O₁, O₂).
O₁O₂=16 см
O₂A>O₁A
1) Окружности касаются внешним образом.
В этом случае отрезок, соединяющий центры, является суммой радиусов.
O₁A+O₂A=O₁O₂
O₁A=x, O₂A=3x
x+3x=16 <=> 4x=16 <=> x=4 (см)
O₁A=4 см
O₂A=3*4 =12 см
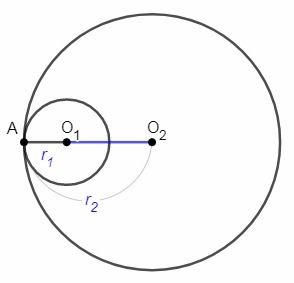
2) Окружности касаются внутренним образом.
В этом случае отрезок, соединяющий центры, является разностью радиусов.
O₂A-O₁A=O₁O₂
O₁A=x, O₂A=3x
3x-x=16 <=> 2x=16 <=> x=8 (см)
O₁A=8 см
O₂A=8*3 =24 см