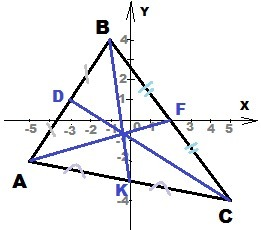
А(-5;-2),B(-1;4),C(5;-4)
D - середина отрезка AB ⇒
AD = DB

D(-3;1) ⇒ Длина медианы CD - расстояние между точками C и D

K - середина отрезка AC ⇒ AK = KC

K(0;-3) ⇒ Длина медианы BK - расстояние между точками B и K

F - середина отрезка BC ⇒ BF = FC

F(2;0) ⇒ Длина медианы AF - расстояние между точками A и F

Длины медиан √89; √53; 5√2