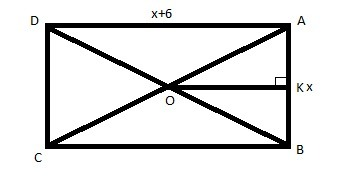
1) 2(х+х+6)=36
4х=24
х=6 следовательно вторая сторона равна 6+6=12
2) Рассмотрим треугольник ABD-прямоугольный, т.к. ABCD-прямоугольник
BD=корню(AD^2+AB^2)=корню из(144+36)=6 корней из 5
3) Рассмотрим треугольник AOB-равноб., т.к О-середина диагоналей;
ОК-высота следовательно ОК-медиана следовательно AK=3
4) Рассмотрим треугольник АОК-прямоуг., т.к. ОК-высота
По теореме Пифагора ОК= корню из(АО^2-OK^2)= корню из(45-9)=6
Ответ:6