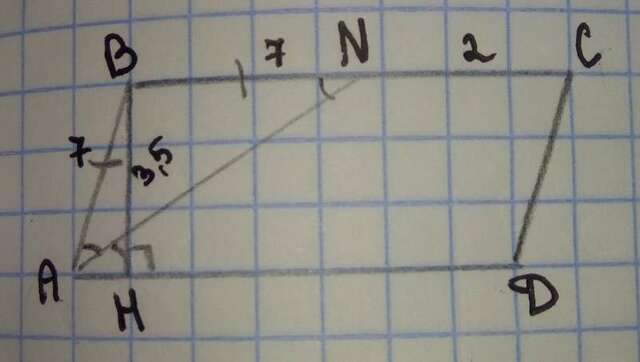В параллелограмме ABCD угол A равен 30, а его биссектриса делит сторону BC ** отрезки 7...

Question

В параллелограмме ABCD угол A равен 30, а его биссектриса делит сторону BC на отрезки 7 см и 2 см, считая от вершины тупого угла. Найдите площадь параллелограмма.

Answer 1

Дано:
ABCD - параллелограмм
AN - биссектриса
BN = 7 см
CN = 2 см
A = 30°
Найти:
S

Решение:
AB = BN = 7 см (биссектриса параллелограмма отсекает равнобедренный треугольник)
Построим высоту BH на сторону AD
ABH - прямоугольный
BH = 0,5 × AB = 3,5 см (катет лежащий против угла в 30° равен половине гипотенузы)
AD = BC = BN + CN = 7 + 2 = 9 см (по свойству параллелограмма)
S = BH × AD = 3,5 × 9 = 31,5 см²

Ответ: 31,5 см²

---