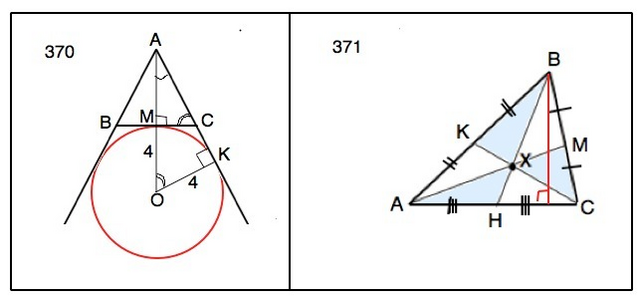
370). Окружность радиуса 4 см касается стороны и продолжений двух других сторон равностороннего треугольника. Найдите его площадь.
Обозначим треугольник ВАС. Вневписанная окружность с центром О касается стороны ВС и продолжений сторон АВ и АС
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. ∆ ВАС - равносторонний. ⇒
∠ВАО=∠САО=60°:2=30°
Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∆ АКО - прямоугольный с острым углом КАО=30°
Катет КО противолежит ему и равен половине гипотенузы.⇒
АО=2 КО=8 см.
АМ=АО-МО=8-4=4 см.
АМ - высота равностороннего ∆ ВАС.
Формула площади правильного треугольника через высоту
S=h²/√3
S=4²/√3=16/√3 см²
--------------
371). Внутри данного треугольника АВС найдите такую точку Х, чтобы площади треугольников АВХ, ВСХ, АСХ были равны.
Искомая точка - точка пересечения медиан треугольника.
Каждая медиана треугольника, взятая по отдельности, делит его на два равновеликих, т.е. равной площади.
Действительно, в ∆ АВС высота ∆ АВН и ∆ СВН из вершины В - общая, основания АН=СН, следовательно, их площади равны. Аналогично АМ и СК делят треугольник на равновеликие части.
Три медианы делят треугольник на 6 равновеликих треугольника. Взятые по два при каждой из сторон, эти треугольники образуют треугольники АВХ, ВСХ и АСХ равной площади.