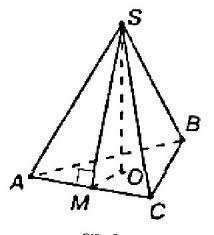
! Площадь бок. поверхности прав. пирамиды равна произведению половины периметра основания на апофему, т.е.
S бок= 0,5·Р осн·SM
1)По условию SO=√6,SA=3√2.
Из Δ АОS-прямоуг.: АО=√АS²-SO²=√(3√2)²-(√6)²=√18-6=√12.
2) Из Δ АВС-правильный: АО- радиус описанной окружности.!Сторона правильного тр-ка равна произведению радиуса описанной окружности на √3, т.е.
АС=АО·√3=√12·√3=√36=6, тогда Р = 3·6=18.
3) найдём апофему SM из прям. тр-ка АМS:
SM= √AS²-AM²=√(3√2)²-3²=√18-9=√9=3 .
4) S бок= 0,5·Р осн·SM= 0,5·18·3=27 (кв.ед.)