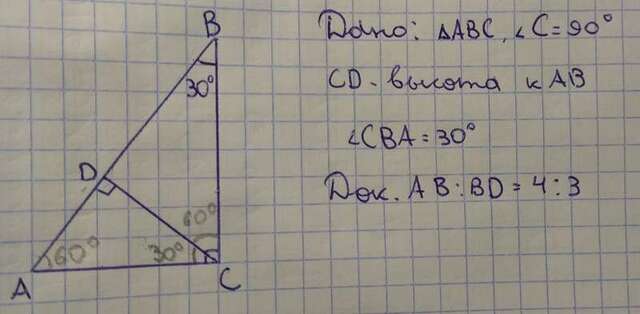
Чертёж и дано во вложении. итак, рассмотрим треугольник АВС. по теореме о сумме острых углов прямоугольного треугольника угол ВАС равен 90°-30°=60°. тогда угол DCA равен 90°-60°=30° по той же теореме, а угол DCB равен 90°-30°=60°(вычитаем известную часть из прямого угла С). у нас есть два угла по 30°, и мы знаем, что катет, лежащий напротив угла в 30°, равен половине гипотенузы. отсюда АС=0,5АВ и АD=0,5AC. объединив эти выражения, можем сделать вывод, что АD=0,5(0,5AB)=0,25AB. 0,25=1/4, значит, на весь отрезок АВ из 4 часей приходится только 1 часть АD. но ведь АВ состоит ещё и из DB, который, соответственно, составляет 4-1=3 части от АВ. то есть, АВ:ВD=4:3, что и требовалось доказать.