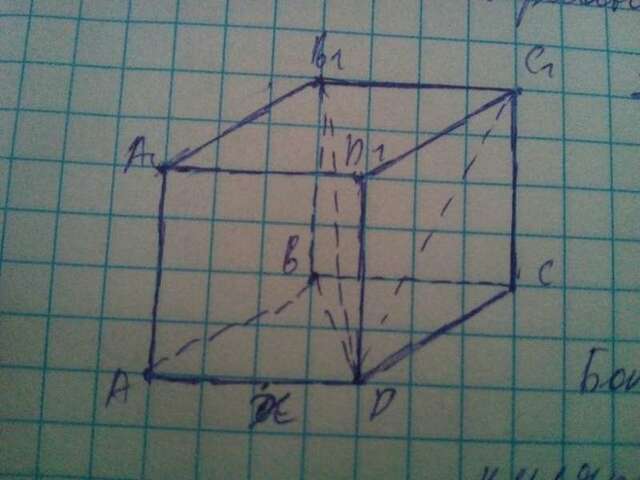
Сторона основания правильной четырехугольной призмы равна 4, диагональ призмы образует с плоскостью основания угол 45°. Найдите:
а) Диагональ призмы
б) Угол между диагональю призмы и плоскостью боковой грани
в) Площадь боковой поверхности призмы
г) Площадь сечения призмы плоскостью, проходящей через сторону нижнего основания и противоположную сторону верхнего основания.
Нужно с решением.