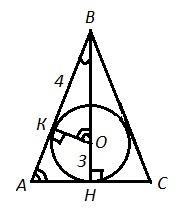
ΔАВС - равнобедренный, АВ=ВС , вписанная окр. r=ОН=ОК=3 cм
ВН - высота ΔАВС ⇒ ΔАВН - прямоугольный, ∠АНВ=90°,
ΔВОК - прямоугольный, т.к. ∠ВКО=90° (как радиус впис. окр., проведённый к стороне Δ).
ΔАВН ~ ΔВКО по двум углам, т.к. ∠АВН - общий, а ∠ВАН=∠ВОК=90°-∠АВН.
По теореме Пифагора ВО=√(ВК²+ОК²)=√(4²+3²)=5
⇒ ВН=ВО+ОН=ВО+r=5+3=8 (cм)
Из подобия следует пропорциональность соответствующих сторон:
ВК:ВН=ОК:АН=ВО:АВ ⇒ 4:8=3:АН=5:АВ ⇒ АН=6 , АВ=10.
АС=2*АН=2*6=12 , т.к. высота ВН явл. ещё и медианой.
tg∠ВАС=ВН/АН=8/6=4/3 ⇒ ∠ВАС=arctg4/3
Радиус описанной окружности найдём из формулы:  .
.
S=1/2*АС*ВН=1/2*12*8=48 (см²)
R=(10*10*12)/(4*48)=6,25 (см)