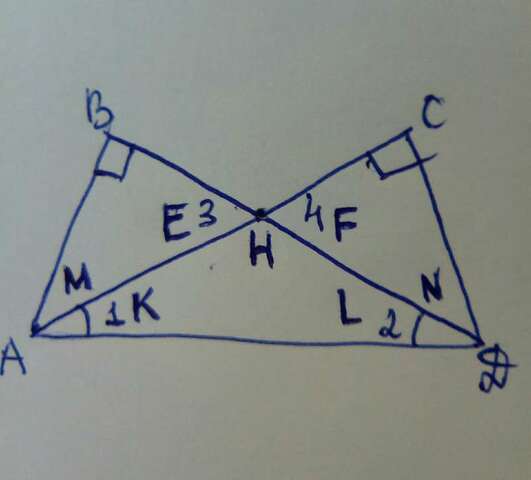
1.( В этой задачи нужно углы ещё как то назвать. Что бы понять , что я потом писала, сравнивай с фото) По условию угол 1 = углу второму, значит треугольник KHL равнобедренный, следовательно ME=FN. Рассмотрим треугольники BEM и CFN. Они равны по второму признаку равенства треугольников: УголB= углу С= 90°, Угол Е= углу F , ME=FN. Соответственно AB=CD, что и требовалось доказать.
2. По условию AB=CD, BC=AD, значит АВСD — параллелограмм. Следовательно AD параллельно BC, АВ параллельно CD. Исходя из этого, угол EDC = углу ABF как накрест лежащие. Рассмотрим треугольники ABF и CDE. Они равны по второму признаку равенства треугольников: угол AFB= углу CED= 90° по условию, угол ABF= углу CDE как накрест лежащие при пересечении секущей BD двух параллельных прямых, AB=CD по условию. Аналогично, что BF=DE, AF=CE, что и требовалось доказать.