Основанием пирамиды PABCD является ромб ABCD с меньшей диагональю AC. Ребро PD...

Question

Основанием пирамиды PABCD является ромб ABCD с меньшей диагональю AC. Ребро PD перпендикулярно плоскости основания.
а) Постройте сечение пирамиды плоскостью, параллельной AC и проходящей через вершину D и середину M ребра PB.
б) Найдите расстояние между прямыми CD и PB, если BC=5SQRT(2), PD=12, угол ABC=45 градусов.

Answer 1

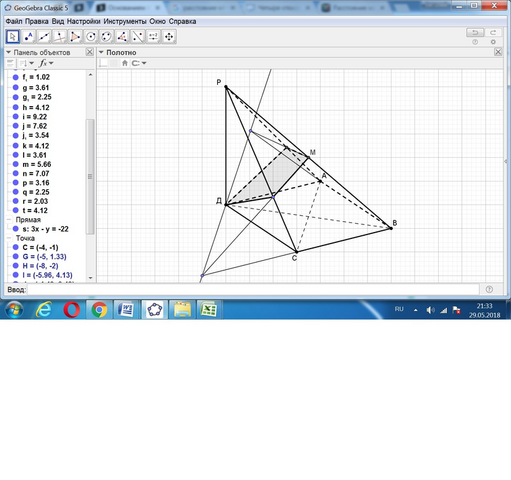
1) Сечение приведено в приложении.
    Основное: след секущей плоскости проходит через точку Д параллельно диагонали ромба АС.

2) Для этого проводим плоскость, параллельную СД, через прямую РВ.
Это - боковая грань РАВ. Её след сечения плоскости основания (АВ) параллелен СД.
Теперь проведём секущую плоскость через точку Р, перпендикулярно РАВ.
В сечении имеем прямоугольный треугольник РДК.
Отрезок РД по заданию равен 12.
Перпендикуляр ДК к прямой, включающей сторону АВ, равен 5√2*cos 45° = 5√2*(√2/2) = 5.
Гипотенуза РК = √(12² + 5²) = √(144 + 25) = √169 = 13.
Тогда искомое расстояние от прямой СД до прямой РВ - это высота ДЕ в треугольнике РДК.
По свойству высоты из прямого угла ДЕ = (12*5)/13 = 60/13 ≈ 4,615385.

---