f(x)=2x^2-7x+6 = 2(x^2 - 7/2x) + 6 = 2(x^2 - 2*x *7/4 + 49/16 - 49/16) + 6 = 2(x-1,75)^2 - 0,125
1) D(y) = R
E(y) = [-0,125; + ∞)
2)Так как из 1-ого пункта следует, что Область определения симметрична, значит можно рассматривать функцию на чётность.
f(-x) = 2(-x)^2 - 7(-x) + 6 = 2x^2 + 7x + 6 - функция общего вида.
Функция возрастает на [1,75;+∞)
Функция убывает на (-∞;1,75]
Функция ограничена снизу. Нижняя граница у = -0,125
3) Пересечение с осью Ох:
2x^2 - 7x + 6 = 0
D = 49 - 48 = 1
x1 = (7+1)/4 = 2 => B(2;0)
x2 = (7-1)/4 = 1,5 => C(1,5;0)
Пересечение с осью Оу:
х = 0 => f(x) = 6 => A(0;6)
4)f(x)>0 => x∈R
f(x) < 0 => x∈∅
5)Асимптот у графика нет.
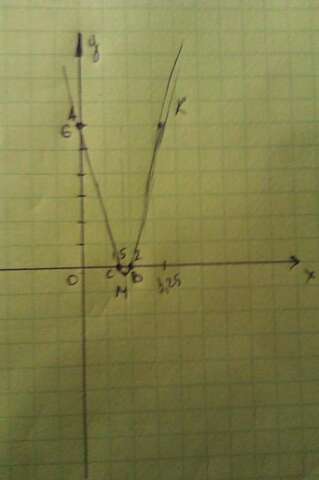
6) График построен на фото!!