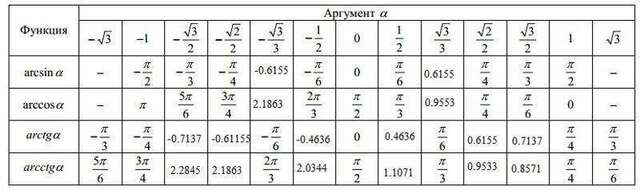
Посмотрим таблицу :
otvet . imgsmail . ru /download/212520366_1e57a2e963deb19ee1b4cafb0f9426b7_800.jpg
Все функции периодичны, поэтому в ответе дописываем период 2π*n или n*π, где n∈Z
arcctg(-1) = 3/4 * π + n*π
arcctg(0) = 1/2 * π + n*π
arcctg(√3 / 3) = 1/3 * π + n*π
С-20
1 a) подставим и посчитаем 3/4 * π + 1/3 * π + 1/2 * π = 19/12 * π + n*π
1 б) 1/√2 если умножить числитель и знаменатель на √2 то 1/√2 = √2/2
arccos(1/√2) = arccos(√2/2) = 1/4 * π по таблице
ctg( arccos(1/√2) ) = ctg( 1/4 * π ) = 1
1 в) arctg( cos(π) ) = arctg( -1 ) = -1/4 * π + n*π
2 a) ctg(x) = -1
x = arcctg(-1) = 3/4 * π + n*π
2 б) tg(x) = 1/6 т.к. нет табличного такого тангенса, то просто пишем арктангенс 1/6
x = arctg(1/6) + n*π